[영상처리] 영상의 특징값 추출 방법

영상의 특징값

• 특징값(feature) :영상 내에서 다른 부분과 구분되어 두드러지는 성질
• 점(point)
• 엣지(edge, 경계선, 외곽선)
• 코너(corner, 모서리)
• 질감(texture)
• 색상(color)
• 특징값은 영상 내에서 특정 사물의 위치를 찾는데 사용될 수 있고, 특정 영상과 다른 영상의 유사성을 판단 하는 기준으로도 사용 될 수 있음

마스크를 이용한 엣지 검출

• 이산 함수의 미분 근사 방법

엣지(edge) 

• 배경과 객체의 경계가 되는 부분으로, 일반적으로 엣지에서 는 픽셀의 밝기 값이 급격하게 변함

함수의 1차 미분(1st derivative) 

• 함수 f(x, y)의 x 축 방향으로의 미분
• 값의 변화량 = 기울기 사용해서 미분함
• 영상 미분 -> 특정한 임계값 t 보다 큰 부분이 엣지임

1차 미분의 근사화(approximation)

• 미분은 연속함수에서만 실행
• 이산함수에 해당하는 영상에 적용하기 위해 근사화 필요함
• h = 픽셀간의 간격 = 1

영상의 그래디언트(gradient)

• 함수 f(x, y)를 x축과 y 축으로 각각 편미분(partial derivative) 하여 벡터 형태로 표현한 것
• 벡터 형태로 표현했기에 그레디언트의 크기와 방향 성분 표현이 가능

• 그레디언트 크기는 변화의 정도를 나타내는 척도
• 그래디언트 방향은 그레디언트 벡터가 가르키는 방향, 경사가 가장 심한 방향, 변화의 정도가 가장 심한 방향

다양한 엣지 검출 마스크

• 로버츠: 2x2 마스크, 대각선 방향
• 프리윗: 3x3 마스크, 세로나 가로 방향
• 소벨: 3x3 마스크, 가중치를 줌으로써 엣지 뚜렷하게 검출됨

단점

• 엣지 주변의 여러 픽셀들이 한꺼번에 엣지로 검출
• 엣지가 이어지지 않고 끊어지는 부분이 있음

캐니 엣지 검출기

좋은 엣지 검출기의 조건 (J. Canny)

• 정확한 검출(Good detection):  엣지가 아닌 점을 엣지로 찾거나 또는 엣지인 점을 검출하지 못하는 확률을 최소화해야 한다.
• 정확한 위치(Good localization):  실제 엣지의 중심을 찾아야 한다. 
• 단일 엣지(Single edge): 하나의 엣지는 하나의 점으로 표현되어야 한다.

-> 이러한 조건을 만족하는 새로운 형태의 엣지 검출 방법을 제안 "캐니 엣지 검출기"

소별 엣지 검출 방법이 단순히 그래디언트 크기만을 이용해 엣지 픽셀을 찾았음....

 

캐니 엣지 검출기의 특징

• 그래디언트의 크기와 방향을 모두 고려함 -> 정확하게 엣지의 위치를 찾을 수 있음 
• 엣지의 진행 방향에 또 엣지가 나타날 가능성이 높다는 점을 고려함 -> 그레디언트가 다소 약하게 나타나는 엣지 픽셀도 놓지지 않을 수 있음
• 그래디언트 크기가 크다 = 기울기가 크다 = 엣지이다. 
• 그래디언트는 함수를 편미분하여 벡터로 표현한 것으로, 방향과 크기를 갖는 기울기임 !! 

캐니 엣지 검출 방법

1. 가우시안 필터링 : 영상 부드럽게 만들기 참조
2. 그래디언트 계산 : 주로 소벨 마스크를 사용
3.  비최대 억제 (Non-maximum suppression) : 하나의 엣지가 여러 개의 픽셀로 표현 되는 현상을 없애기 위하여 그래디언트 크기가 국지적 최대(local maximum)인 픽셀만을 엣지 픽셀로 설정 /  그래디언트의 방향 성분을 고려하여 국지적 최대를 검사
4. 히스테리시스 엣지 트래킹 : 두 개의 임계값을 사용: TLow, THigh /  강한 엣지: 그래디언트 크기가 THigh보다 큰 픽셀 → 최종 엣지로 선정 / 약한 엣지: TLow보다 크고 THigh보다 작은 픽셀 → 강한 엣지와 연결되어 있는 픽셀만 최종 엣지로 선정

허프 변환을 이용한 직선 검출(직선 성분 찾는 알고리즘)

허프 변환(Hough transform) 

• 2차원 영상 좌표(xy공간)에서의 직선의 방정식을 파라미터 (parameter) 공간(ab공간)으로 변환하여 직선을 찾는 알고리즘

• xy 공간에서 a는 기울기이고, b는 y절편
• 이 직선의 방정식은 2차원 xy 좌표 공간에서 정의
• a와 b는직선의 모양을 결정하는 파라미터

2차원 xy 공간에서의 직선의 방정식을 파라미터 공간인 ab 공간으로 변형하면???

• 2차원 xy 공간에서의 직선 -> ab 공간에서 한 점
• 2차원 xy 공간에서 한 점 -> ab 공간에서 직선
• 허프 변환은 이런 현상을 이용해서 xy 공간에서 엣지 좌표를 허프 공간에서 직선 형태로 찾음
• 2차원 xy 공간에서 점 -> 파라미터 공간에서 두 직선은 서로 같은 직선에 존재했었기 때문에 교차점을 가짐 -> 이 교차점은 2차원 xy 공간에서 (기울기, y 절편)
• 즉 많은 수의 직선들이 교차할수록 원래 2차원 xy 공간에서 같은 직선에 존재했던 점이 많다는 소리

축적 배열

• 일반적인 2차원 배열을 이용하여 만든 후, 해당 직선 성분의 값을 1씩 증가시키는 배열(직선이 지나가는 위치의 배열 원소값 +1)
• 허프 변환을 통해서 직선의 방정식을 찾기 위해서는 xy 공간에서 엣지로 판명된 모든 점의 좌표를 ab 파라미터 공간에서 직선으로 그려주고, 직선들이 많이 교차되는 점을 찾으면 됨
• 이때 직선이 교차하는 점을 찾기 위해 "축적 배열" 사용

직선의 방정식 y = ax + b 를 사용할 때의 문제점 

• y 축과 평행한 수직선을 표현하지 못함 ➔ 극좌표계 형태의 직선의 방정식을 사용

해리스 코너 포인트 

해리스 코너 포인트 검출 방법 

• 1988년 C. Harris가 제안한 방법 
• 영상 내에 정의된 윈도우(window)안의 픽셀 값이 상하좌우 방향으로 모두 급격하게 변하는 위치를 코너로 규정

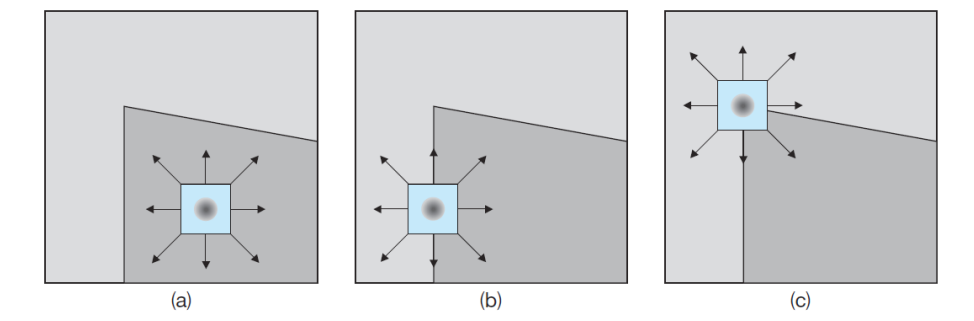
코너 응답 함수(corner response function)

실제 영상에서 해리스 코너 포인트 검출 결과

• 영상의 크기, 회전 등의 기하학적 변환에 무관하게 코너 포인트를 검출 
• 다양한 영상 처리 분야에서 특징점 (feature point) 검출 방법으로 사용