[데이타베이스론] 데이타 종속성과 정규화

데이타의 논리적 표현

릴레이션 스키마의 설계

• 논리적 데이타베이스 설계
• 관계 모델을 이용하여 어떻게 실세계를 정확히 표현할 것인가?

 i.  애트리뷰트, 엔티티, 관계성을 파악(현실 세계에 있는 것들을 바탕으로)

ⅱ. 관련된 애트리뷰트들을 릴레이션으로 묶음(테이블 형태로 만든다.)

*고려사항

1.애트리뷰트들간의 관계성(relationship): 데이타 종속성(data dependency)

2.효율적인 데이타 처리

3.데이타의 일관성

 iii.  변칙적 성질의 예방(애트리뷰트의 종속성에 의한 이상을 방지해야 한다.)

데이타 변경 시의 이상(anomaly)

이 테이블에서는 불필요한 학년이 있어서 이상 현상이 발생함

이상

삭제 이상

• 200번 학생이 'C123'의 등록을 취소

   ⇒ 3학년이라는 정보도 함께 삭제됨

• 연쇄 삭제(triggered deletion)에 의한 정보 손실(loss of information)

삽입 이상

• 600번 학생이 2학년이라는 사실을 삽입

    ⇒ 어떤 과목을 등록하지 않는 한 삽입이 불가능

          (∵ 과목 번호가 기본 키)

• 원하지 않는 정보의 강제 삽입

갱신 이상

• 400번 학생의 학년을 4에서 3으로 변경

   ⇒ 학번 400에 대한 4개의 투플 모두를 변경해야 함

• 중복 데이타의 일부 갱신으로 정보의 모순성(inconsistency)이 발생

이상의 원인과 해결책

• 이상의 원인 : 하나의 개체에 속한 애트리뷰트들 간에 존재하는 여러 개의 종속관계 (dependency)를 하나의 릴레이션으로 표현하기 때문
•  
   => 하나의 종속성은 하나의 릴레이션으로 표현
          ⇒ 정규화(normalization) 과정
• 이상의 해결 : 애트리뷰트들 간의 여러 종속관계를 분해(decomposition) 하여 각각 하나의 릴레이션으로 표현

스키마 설계와 변환

스키마 설계 : 데이타베이스의 논리적 설계

① 애트리뷰트들과 이들의 제약조건 (종속성)들을 수집

② 수집된 결과를 명시된 제약조건에  따라 바람직한 여러 개의  릴레이션으로 분할

⇒ 스키마 변환 (schema transformation)

스키마 변환의 원리

① 정보 표현의 무손실(nonloss representation of information) - 개선된 구조

② 최소의 데이타 중복(minimal data redundancy)

③ 분리의 원칙(principle of separation) - 독립된 관계성은 별도의 릴레이션으로 분리시켜 표현

 

함수 종속(FD)

함수 종속(functional dependency: FD)의 정의

• 어떤 릴레이션 R에서,  애트리뷰트 X의 값 각각에 대해 애트리뷰트 Y의 값이 최대 하나만 연관

<-> 애트리뷰트 Y는 애트리뷰트 X에 함수 종속  X -> Y

• 애트리뷰트 X는 Y를 (함수적으로) 결정
• X를 결정자(determinant)
• Y를 종속자(dependent)
• X나 Y는 각각 두 개 이상의 애트리뷰트 집합이 될 수 있음
• 릴레이션 R에서 애트리뷰트 X가 키이면,(기본키)
      R의 모든 애트리뷰트 Y에 대해 X -> Y 성립
• 함수종속 X -> Y의 경우
      애트리뷰트 X가 반드시 키(유일 값)라는 것을  요건으로  하지 않음
•  즉, X의 어느 한 값에 대응되는 Y 값을 갖는 투플이 둘 이상 존재 가능

함수 종속 다이어그램

• 함수 관계의 표현
• 수강 릴레이션: 수강(학번, 과목번호, 학년, 성적)

        기본 키: { 학번, 과목번호 }

          {학번, 과목번호} -> 성적

          학번 -> 학년

완전 함수 종속과 부분 함수 종속

• 2개 이상으로 구성된 애트리뷰트 집합 X에 대하여 X -> Y가 성립할 때
• 완전 함수 종속 문제는 결정자가 두개 이상의 애트리뷰트로 구성된 경우에만 일어날 수 있음
• 릴레이션 R의 어떤 애트리뷰트 Y가 다른 애트리뷰트 X에 함수 종속일 때 !!

X의 진부분 집합에는 함수 종속이 아닐 때 Y는 X에 완전 함수 종속, 진부분 집합 부분에 대해 Y가 함수 종속일 때 부분 함수 종속

함수 종속에 대한 추론 규칙

• 함수 종속은 데이타의 의미(data semantics) 를 표현

예: “학번 -> 학년”의 의미는 “학생은 한 학년에만 속한다”

의미적 제약조건(semantic constraint) & 데이타 베이스가 항상 유지해야 될 조건

•  DBMS는 함수 종속을 유지하기 위하여 함수 종속을 스키마에 명세하는 방법과  함수 종속을 보장하는 방법을 제공해야 함

기본 정규형

정규형(제1~5)

• 어떤 일련의 제약조건(constraints)을 만족하는 릴레이션
• 제약조건은 보통 함수의 종속을 의미
• 서로 독립적인 관계는 별개의 릴레이션으로 표현해야 한다 !!
• 정규화(normalization) 즉 스키마 변환 (S -> S')으로 정규형을 만듦
• 차수가 높아질수록 만족시켜야 할 제약조건이 가중됨

정규화의 원칙

① 정보 표현의 무손실

• 같은 의미의 정보 유지
• 효율적인 구조

② 최소의 데이타 중복

③ 분리의 원칙

• 독립적인 관계는 별개의 릴레이션으로 표현
• 릴레이션 각각에 대해 독립적 처리가 가능

---

제1정규형 

• 모든 도메인이 원자 값(atomic value)만으로 된 릴레이션
• 모든 정규화 릴레이션은 제1정규형에 속함

예 :  수강지도 릴레이션

• 수강지도 (학번,지도교수,학과,과목번호,성적)
• 기본 키 : {학번,과목번호}
• 함수 종속 : {학번,과목번호} -> 성적

                           학번 -> 지도교수

                           학번 -> 학과

                           지도교수 -> 학과

1NF에서의 어떤 이상이 존재하나요????

• 삽입 이상은 하나의 기본키 값만 삽입하면 다른 기본키는 null값이 되므로, 삭제와 갱신 이상은 기본키 1+ 다른 애트리뷰트 값 지우려면 다른 부속 정보까지 삭제되거나 갱신해야 함

① 삽입이상

• 500번 학생의 지도교수가 P4라는 사실을 삽입하려 할 때 어떤 과목을 등록하지 않는 한 삽입은 불가능

② 삭제이상

• 200번 학생이 C123의 등록을 취소하여 이 투플이 삭제되는 경우에 지도교수가 P2라는 정보까지 손실됨

③ 갱신이상

• 400번 학생의 지도교수를 P1에서 P3로  변경하는 경우에 학번이 400인 4개의 투플에 대한 지도교수를 모두 P3로 변경해야 함

1NF 이상의 원인

• 기본 키에 부분 함수 종속된 애트리뷰트가 존재

       -> 기본 키로 식별되는 개체와 무관한 애트리뷰트가 존재

       -> 두 가지 독립적인(상이한) 정보가 하나의 릴레이션으로 표현

1NF 이상의 해결

• 프로젝션으로 1NF 릴레이션을 분해 (부분 함수 종속을 제거) ⇒ 2NF

---

제 2정규형(2NF)

• 1NF이고, 키에 속하지 않는 애트리뷰트들은 모두 기본 키에 완전 함수 종속

• 프로젝션은 관계형 데이터베이스에서 사용되는 용어로, 릴레이션(테이블)에서 원하는 속성(열)들을 선택하여 새로운 릴레이션을 생성하는 작업을 말합니다. 이때 생성된 새로운 릴레이션을 "프로젝션된 릴레이션"
• 정규화된 제 1정규형에서 완전 함수 종속이 되도록 원하는 열만 선택해서 "프로젝션된 릴레이션"들로 만들면 제 2정규형
• 완전 함수 종속처럼 분해된 제 2정규형들을 다시 합치는 "조인"을 실행하면 제 1정규형
• 1NF 수강지도 릴레이션 / 2NF 수강 릴레이션과 지도 릴레이션
• 하나의 릴레이션을 아무런 정보 손실 없이 동등한 릴레이션으로 분해 "무손실 분해"

예 :  수강지도 ⇒ 지도, 수강 릴레이션으로 분해

 

원래의 제 1정규형은 부분 함수 종속이 발생했어서 그것을 제거한 게 제 2정규형이다.

2NF에서의 이상

① 삽입이상

• 어떤 지도교수가 특정 학과에 속한다는 사실의 삽입이 불가능

② 삭제이상

• 300번 학생의 투플을 삭제하면 지도교수 P3가 컴퓨터공학과에 속한다는 정보를 상실

③ 갱신이상

• 지도교수 P1의 소속을 컴퓨터공학과에서 전자과로 변경한다면 학번이 100과 400인 두개의 투플을 모두 변경해야 함

2NF 이상의 원인

• 이행적 함수 종속이 존재
• 릴레이션 R에 함수 종속 A -> C가 존재하고 함수 종속   A -> B와 B -> C가 성립할 때 애트리뷰트 C는 애트리뷰트 A에 이행적 함수 종속이라고 한다.

2NF 이상의 해결

• 프로젝션으로 2NF 릴레이션을 분해 (이행적 함수 종속을 제거)⇒ 3NF
• 원하는 애트리뷰트만 프로젝션으로 다시 뽑아내서 새로운 릴레이션 만들어라

---

제 3정규형

• 2NF이고, 키가 아닌 모든 애트리뷰트들은  기본 키에 이행적 함수 종속이 되지 않음

이행적 함수 종속을 제거했음

• 키가 아닌 애트리뷰트 값의 갱신 시 불필요한 부작용 (이상)은 발생하지 않음
• 제 3정규형에 속하는 릴레이션에 대해서 DBMS가 알아야 될 종속성은 기본 키를 구성하는 애트리뷰트에 관한 것뿐
• 왜냐면 제 3 정규형에 관련된 종속 관계는 기본 키와 관련된 종속 관계뿐이므로
• 모든 이원 릴레이션은 3NF에 속함

3NF의 약점

• 하나의 기본키만 가진 것으로 정의했음. 여러 개의 기본 키 적용 x

-- 적용할 수 없는 경우

i   .  복수의 후보 키를 가지고 있고

ii  .  후보 키들이 두 개 이상의 애트리뷰트들로 구성되고

iii .  후보 키들의 애트리뷰트가 서로 중첩되는 경우

⇒ 보다 일반적인 Boyce/Codd Normal Form(BCNF)을 제안

이행적 함수 종속처럼 보일 수도 있지만, 아님 !! 완전 함수 종속 & 이행적 함수 종속x면 제 3 정규형이라고 한다.

---

보이스/코드 정규형(BDNF)

• 릴레이션 R의 결정자(determinant)가 모두 후보 키이면 릴레이션 R은 BCNF에 속한다.
• 강한 제 3정규형이라고도 함
• 릴레이션 R이 BCNF에 속하면 R은 제1, 제2, 제3 정규형에 속함(완전 함수 종속, 이행적 함수 종속x, 결정자가 후보키)

결정자인 교수를 후보키로 지정함

 

정규형들 간의 관계

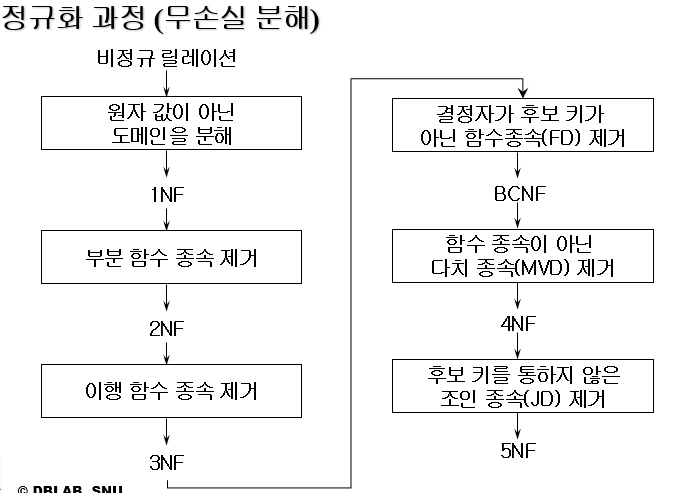
• 릴레이션의 정규화는 실제 데이타 값이 아니라  개념적인 측면에서 다루어져야 함
• 실제 정규화 과정은 정규형의 순서와는 일치하지 않을 수 있음

퀴즈(pdf 53~)

• 릴레이션에서 같은 투플에 있는 기본키의 값이 아닌 속성을 삭제하는 것은 일반적으로 상관없습니다. 삭제된 속성은 해당 투플에 null 값으로 표시될 수 있습니다. 그러나 기본키의 값은 삭제되는 것이 아니라 유지됩니다.-> 데이타 일관성 유지 ㄱㄴ
• X값을 넣었을때 동일한 Y가 나온다면 종속성이 인정된다고 보았습니다.